| Infomration | Value |
|---|---|
| Contest Link | LeetCode Weekly Contest 313 |
| Date | 2022-10-01 |
| Why Taking this course? | Data Structure and Algorithm is the foundation for software engineer |
| Summary | AC Q1 Q2 ; Q3 WA once ; Q4 TLE once |
| Ranking | 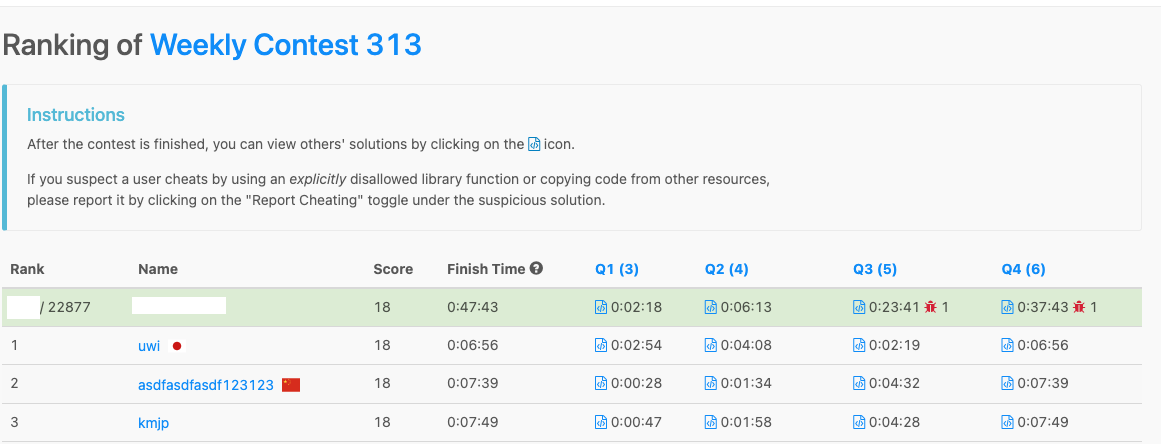 |
Summary
This week I joined my LeetCode competition and luckily AC all 4 questions eventually. The first three questions are quite straightforward and are completed within the first 23 mins. The 4th question is a little bit tricker but still made to AC at 37 min. The forth question itself is clearly a DP problem but the complexity of DP solution is still O(n^2), and given the n can be as large as 4000, the n^2 can easily go to 1.6x10^7 and likely to TLE (which is the reason why I failed once).
Question 2430. Maximum Deletions on a String
You are given a string s consisting of only lowercase English letters. In one operation, you can:
- Delete the entire string s, or
- Delete the first i letters of s if the first i letters of s are equal to the following i letters in s, for any i in the range `1 <= i <= s.length / 2`.
For example, if s = "ababc", then in one operation, you could delete the first two letters of s to get "abc", since the first two letters of s and the following two letters of s are both equal to "ab".
Return the maximum number of operations needed to delete all of s.
This question is cleary a DP problem because of the following two features 1. it’s asking for the maximum of xxx and 2. there is clearly a recursive relation between Question(n) and Question(n+1), where n here is the index of the string. More specifically:
- The recursion relation is: given a substring
s[i:-1]its maximal number of deletionResult(i)ismax(Result(i+j)) among all eligible jif there is any suchjfor repeated starting substring (this coresponds to deleting the repeated leading substring), or1if no suchjexist (this corresponds to deleting the entire string). - the base case is: if
i==len(s)-1, i.e. if there is only one character in the sub-problem, then the maximum number of deletion is 1. i.e.Result(len(s)-1) = 1.
Given this two relation, I create my first answer
class Solution:
def deleteString(self, s: str) -> int:
N = len(s)
@lru_cache(None)
def dp(s:str) -> int:
if len(s) == 1:
return 1
else:
N = len(s)
r = 0
for j in range(1, N//2+1):
if s[:j] == s[j:2*j]:
r = max(r, 1 + dp(s[j:]))
if r == 0:
r = 1
return r
return dp(s)
Unfortunately, this answer will lead to Time Limit Exceeded error, where the failed test case is aaaa...a (there are 4000 repeated ‘a’). In this case, the answer’s time complexity is maximized to be roughly (0.5x4000)^2 / 2 ~= 0.125 x 1.6 x 10^7.
Working Solution
I tried my luck by adding one edge case check that check if the string is a monotic string with only one type of character at the very begining of DP function, and it’s working, hmm…
if len(set(s)) == 1:
return len(s)
Thoughts and Further Experiments
Although this can walk around the test case and AC this question, I personally don’t think this is a perfect solution, because essentially the problem’s complexity hasn’t been changed and there is still edge case not covered by it (e.g. what if there is a test case with aaaa.....ab, clearly it will still lead to TLE because the monotonic substring condition will never be satisified).
Therefore I did the following experiments to see if we can universally solve this problem (i.e. avoid the TLE) without using the len(set(s)) == 1 checking. In short, although I eventually didn’t find a good solution that can walkaround this test case, some valuable lessons are learnt.
- I firstly tried to change the
DPargument from typestringtoint. The intuition behind it is that Python string is immutable (reference), meaning Python has to initiate a new object for creating substring vias[i:j]and this object initiation can be time-consuming. As a better solution, if we only use the index (i.e. pointer to the starting index of the original string), maybe the time for initiating string can be saved. The experiment support this assumption: the running time is consistently reduced from2600msto1500ms(a40%improvement) for the test case of2000repeated'a'!class Solution: def deleteString(self, s: str) -> int: N = len(s) @lru_cache(None) def dp(i:int) -> int: if i == N-1: return 1 else: sub_string_lenth = N-i r = 0 for j in range(1, sub_string_lenth//2+1): if s[i:i+j] == s[i+j:i+2*j]: r = max(r, 1 + dp(i+j)) if r == 0: r = 1 return r return dp(0) - I secondly tried to convert the string
sto list vias = list(s), it’s a pure experiment because we know there is string comparsions[i:i+j] == s[i+j:i+2*j]and I want to see if list comparison can be faster. Unfortunately that’s not the case. By converting the string to list, the time is significant increased from1500msto4000ms(a 100+% time increment). This finding is later theoretically proved by some reference (link)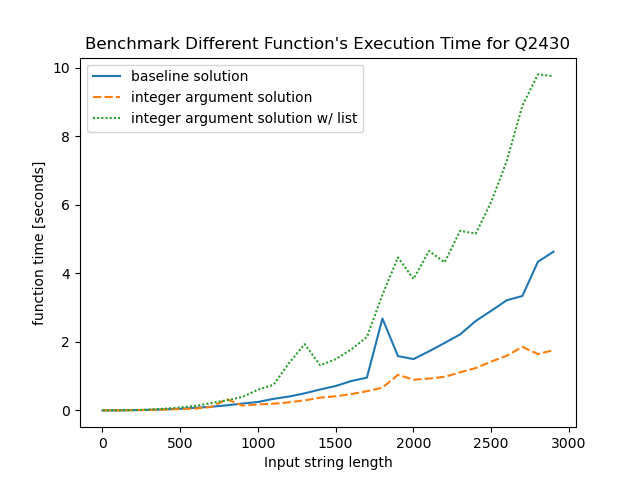
In conclusion, we havne’t fully resolved the edge case of “aaaa..a” without using an explicit checking logic. We learnt that passing point into DP function instead of initiating substring has better performance; we also learnt that string comparsion is faster than list comparsion, thus converting string to list in such use case is not a good practice.
Appendix
- code of benchmarking the 3 method’s computation time
from functools import lru_cache
import sys
sys.setrecursionlimit(10000)
def deleteString_int_argument_solution( s: str) -> int:
N = len(s)
@lru_cache(None)
def dp(i:int) -> int:
if i == N-1:
return 1
else:
sub_string_lenth = N-i
r = 0
for j in range(1, sub_string_lenth//2+1):
if s[i:i+j] == s[i+j:i+2*j]:
r = max(r, 1 + dp(i+j))
if r == 0:
r = 1
return r
res = dp(0)
dp.cache_clear()
return res
def deleteString_baseline_solution( s: str) -> int:
N = len(s)
@lru_cache(None)
def dp(s:str) -> int:
if len(s) == 1:
return 1
else:
N = len(s)
r = 0
for j in range(1, N//2+1):
if s[:j] == s[j:2*j]:
r = max(r, 1 + dp(s[j:]))
if r == 0:
r = 1
return r
res = dp(s)
dp.cache_clear()
return res
def deleteString_int_list_solution(s: str) -> int:
N = len(s)
s = list(s)
@lru_cache(None)
def dp(i:int) -> int:
if i == N-1:
return 1
else:
sub_string_lenth = N-i
r = 0
for j in range(1, sub_string_lenth//2+1):
if s[i:i+j] == s[i+j:i+2*j]:
r = max(r, 1 + dp(i+j))
if r == 0:
r = 1
return r
res = dp(0)
dp.cache_clear()
return res
if __name__ == "__main__":
fun_candidates = {
"baseline solution": deleteString_baseline_solution,
"integer argument solution": deleteString_int_argument_solution,
"integer argument solution w/ list": deleteString_int_list_solution,
}
import time
res = {k:dict() for k in fun_candidates}
for intro, fun in fun_candidates.items():
for i in range(1, 3000, 100):
print(intro, fun, i)
s = "".join(["a"] * i)
start = time.time()
fun(s)
end = time.time()
res[intro][i] = end - start
print(res)
import pandas as pd
res = pd.DataFrame(res)
import seaborn as sns
sns.lineplot(data = res)
from matplotlib import pyplot as plt
plt.ylabel("function time [seconds]")
plt.xlabel("Input string length")
plt.title("Benchmark Different Function's Execution Time for Q2430")
plt.show()