| Infomration | Value |
|---|---|
| Contest Link | LeetCode Weekly Contest 313 |
| Date | 2022-10-08 |
| Why Taking this course? | Data Structure and Algorithm is the foundation for software engineer |
| Summary | AC Q1 Q2 ; Q3 WA twice ; Q4 WA twice |
| Ranking | 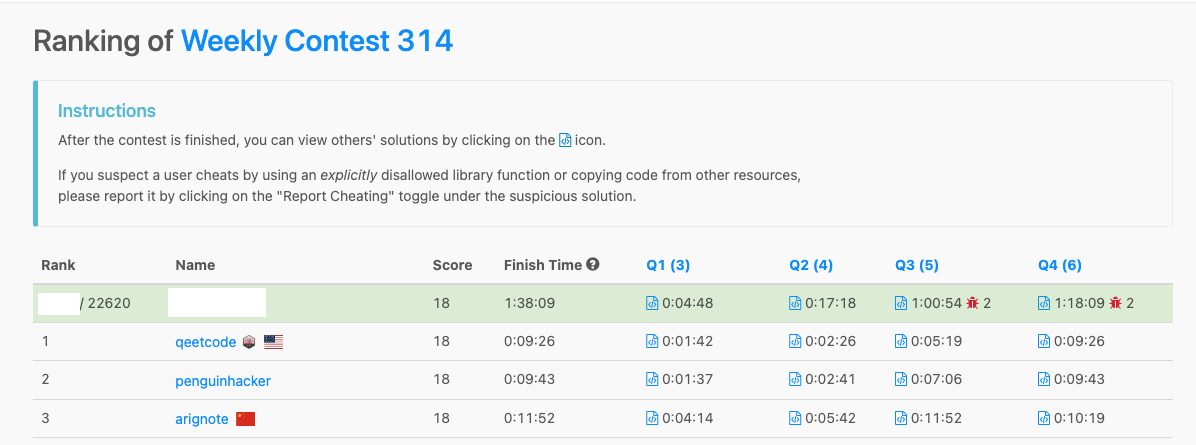 |
Summary
This week I joined my LeetCode Weekly Contest 315 and luckily AC all 4 questions eventually. Among the 4 questions asked, I am most impressed by the 3rd question because it seems not a very standard question that has template we can directly fit the solution in, so I will focus on this question in this blog.
2434. Using a Robot to Print the Lexicographically Smallest String
You are given a string s and a robot that currently holds an empty string t. Apply one of the following operations until s and t are both empty:
Remove the first character of a string s and give it to the robot. The robot will append this character to the string t.
Remove the last character of a string t and give it to the robot. The robot will write this character on paper.
Return the lexicographically smallest string that can be written on the paper.
Example 1:
Input: s = "zza"
Output: "azz"
Explanation: Let p denote the written string.
Initially p="", s="zza", t="".
Perform first operation three times p="", s="", t="zza".
Perform second operation three times p="azz", s="", t="".
Example 2:
Input: s = "bac"
Output: "abc"
Explanation: Let p denote the written string.
Perform first operation twice p="", s="c", t="ba".
Perform second operation twice p="ab", s="c", t="".
Perform first operation p="ab", s="", t="c".
Perform second operation p="abc", s="", t="".
Example 3:
Input: s = "bdda"
Output: "addb"
Explanation: Let p denote the written string.
Initially p="", s="bdda", t="".
Perform first operation four times p="", s="", t="bdda".
Perform second operation four times p="addb", s="", t="".
My Thoughts During Contest
- Firstly, to ensure the result is lexicographically minimum, the smallest character should definitely be the first one in the result. (This can be proved by contradiction with 2 steps: 1. having
min(s)atres[0]is definitely do-able by firstly moving all characters before that fromstot(i.e. first step) and secondly moving the latest character fromttoresult(i.e. second step), and 2. otherwise the result will be larger and doesn’t satisfy the minimum requirement). - The first bullet point is a constrains for my follow-up operations, because I can’t arbitrary extract an character from
tto result unless I remove all the characters after that fromttoresultfirst. I have two choices: - The second bullet point means I have two options: 1) repeat the first bullet for the rest of
s(this is a little bit recursion), I should choose this operation if there there exist a character insthat’s smaller that the last element int2) remove the last character fromttoresult, I should choose this operation if all element insare larger than the last element int.
With this idea, here is the code I submitted during the contest:
class Solution:
def robotWithString(self, s: str) -> str:
if len(s) == 1:
return s
s = list(s)
t = []
N = len(s)
right_min_ch_and_idx = [None] * N
temp = (s[-1], len(s)-1)
for i in range(len(s)-1, -1, -1):
if s[i] <= temp[0]:
right_min_ch_and_idx[i] = (s[i],i)
temp = right_min_ch_and_idx[i]
else:
right_min_ch_and_idx[i] = temp
# right_min_ch_and_idx is a list of same size with `s`, and each element of s is a tuple of size two, where the first element is `min(s[idx:])` and the second elemnt is the `argmin_index(s[idx:])`. The reason why i create this list is for quickly identifying the minimum element on the right size and compare that with the current element to determine if I should continue with operation 1 or 2.
idx = 0
stack = []
res = []
# the invariant among all iteration is that: t[-1] is larger than the minimum element of s[idx:], and s[right_min_ch_and_idx[idx][1]] is the minimum element within s[idx:]
while idx < N:
t.extend(s[idx: right_min_ch_and_idx[idx][1]])
idx = right_min_ch_and_idx[idx][1]
res.append(s[idx])
idx += 1
# print(idx, s, t, res)
if idx >= N:
break
while t and t[-1] <= right_min_ch_and_idx[idx][0]:
res.append(t[-1])
t = t[:-1]
res.extend(t[::-1])
return "".join(res)
Solution Answer
The solution is very similar idea, but the only difference is that, it use a hashmap (key = character, val = remaining character count in s) to get the minimal element in s. This is a smart strategy as the code is much shorter this time.
class Solution:
def robotWithString(self, s: str) -> str:
s = list(s)
# this counter maintain the minimum element in s
cnt = dict(Counter(s))
t =[]
res = []
for c in s:
t.append(c)
if cnt[c] == 1:
del cnt[c]
else:
cnt[c] -= 1
while t and cnt and t[-1] <= min(cnt):
res.append(t.pop())
return "".join(res + t[::-1])
Conclusion & Learning
- This is a greedy solution which I didn’t practice a lot cuz it’s very case-specific. I believe one signature of using greedy solution is that “The solution should definitely be xxxxxx (or start with xxxxxx) to satisfy the requirement”
Counteris our good friend, especially for the case where the key is limited (here the key number is 26 at maximum.)